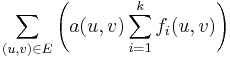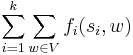Multi-commodity flow problem
The multi-commodity flow problem is a network flow problem with multiple commodities (flow demands) between different source and sink nodes.
Contents |
Definition
Given a flow network 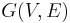 , where edge
, where edge 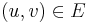 has capacity
has capacity 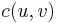 . There are
. There are 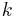 commodities
commodities  , defined by
, defined by 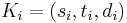 , where
, where 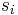 and
and 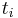 is the source and sink of commodity
is the source and sink of commodity 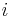 , and
, and  is the demand. The flow of commodity
is the demand. The flow of commodity 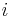 along edge
along edge 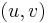 is
is 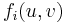 . Find an assignment of flow which satisfies the constraints:
. Find an assignment of flow which satisfies the constraints:
-
Capacity constraints: 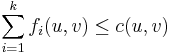
Flow conservation: 
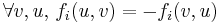
Demand satisfaction: 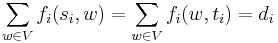
In the minimum cost multi-commodity flow problem, there is a cost 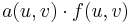 for sending flow on
for sending flow on 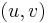 . You then need to minimise
. You then need to minimise
In the maximum multi-commodity flow problem, there are no hard demands on each commodity, but the total throughput is maximised:
In the maximum concurrent flow problem, the task is to maximise the minimal fraction of the flow of each commodity to its demand:
Relation to other problems
The minimum cost variant is a generalisation of the minimum cost flow problem. Variants of the circulation problem are generalisations of all flow problems.
Usage
RWA (Routing Wavelength Assignment) in Optical Burst Switching of Optical Network would be approached via multi-commodity flow formulas.
Solutions
The known solutions to this problem are based on linear programming[1].
The problem is NP-complete[2] for integer flows, even for only two commodities. There exist fully polynomial time approximation schemes for solving the problem within an error bound[3]. For the fractional variant of the problem, a solution is found in polynomial time.
External resources
- Papers by Clifford Stein about this problem: http://www.columbia.edu/~cs2035/papers/#mcf
- Software solving the problem: http://www.zib.de/Optimization/Software/Mcf/
References
- ^ Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001) [1990]. "29". Introduction to Algorithms (2nd ed.). MIT Press and McGraw–Hill. pp. 788–789. ISBN 0-262-03293-7.
- ^ S. Even and A. Itai and A. Shamir (1976). "On the Complexity of Timetable and Multicommodity Flow Problems". SIAM Journal on Computing (SIAM) 5 (4): 691–703. doi:10.1137/0205048. http://link.aip.org/link/?SMJ/5/691/1.
- ^ George Karakostas (2002). "Faster approximation schemes for fractional multicommodity flow problems". Proceedings of the thirteenth annual ACM-SIAM symposium on Discrete algorithms. pp. 166–173. ISBN 0-89871-513-X.